用途
強連結成分分解をする. 巡回可能な部分ごとにグラフを分けてまとめ, それらのDAGを作る.
Example
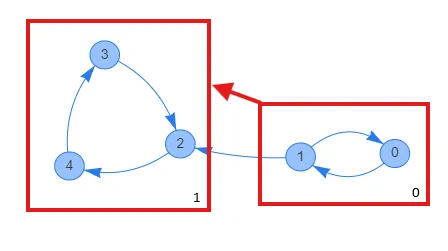
上図においてグループ0とグループ1内ではそれぞれ互いに移動可能であり, またグループ間の移動についてグループ0からグループ1のみに移動可能である. 感覚的にはグラフの圧縮.
計算量
使い方
宣言
auto res = scc(g);gはvector<vector<int>>.
res.indexToContracted[i]で頂点iが属する強連結成分のindexを得る.
res.contractedGraphで強連結成分ごとにまとめられたグラフを得る(vector<vector<int>>).
Exampleでの実行結果は:
res.indexToContracted = { 0,0,1,1,1}res.contractedGraph = { {1}, {}}となる.
実装
struct scc_return { vector<vector<int>> contractedGraph; vector<int> indexToContracted;};scc_return scc(const vector<vector<int>> &_g) { vector<vector<int>> gg(_g.size()), rg(_g.size()), contracted; vector<int> comp(_g.size(), -1), order, used(_g.size()); for (int i = 0; i < _g.size(); i++) { for (auto e : _g[i]) { gg[i].emplace_back(e); rg[e].emplace_back(i); } } auto dfs = [&](auto &&self, int idx) { if (used[idx]) return; used[idx] = true; for (int to : gg[idx]) self(self, to); order.push_back(idx); }; auto rdfs = [&](auto &&self, int idx, int cnt) { if (comp[idx] != -1) return; comp[idx] = cnt; for (int to : rg[idx]) self(self, to, cnt); }; for (int i = 0; i < gg.size(); i++) if (!used[i]) dfs(dfs, i); reverse(order.begin(), order.end()); int ptr = 0; for (int i : order) if (comp[i] == -1) rdfs(rdfs, i, ptr), ptr++; contracted.resize(ptr); for (int i = 0; i < _g.size(); i++) { for (auto &to : _g[i]) { int x = comp[i], y = comp[to]; if (x == y) continue; contracted[x].push_back(y); } } for (auto &v : contracted) { sort(v.begin(), v.end()); v.erase(unique(v.begin(), v.end()), v.end()); } return {contracted, comp};}